Przestrzeń Hilberta

===========================================================

Wektory ∞-wymiarowe mogą być interpretowane jako funkcje, których wartości są składowymi tych wektorów. Przestrzeń ∞-wymiarowe rozpięta na tych funkcjach nazywa się przestrzenią Hilberta.

 

 

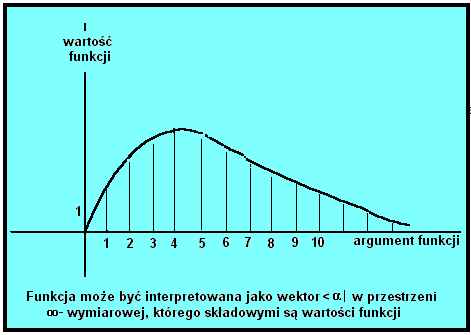
Każdy wektor <a| w tej przestrzeni to funkcja, jeśli zmienna w tej funkcji oznaczona jest x, a sama funkcja np. - y_n (greckie psi) wtedy w istocie wektor w tej przestrzeni może być przedstawiony  w postaci <a _n |=y _n(x), indeks „n” wskazuje, że takich funkcji rozpinających daną ¥ -wymiarową przestrzeń Hilberta może być wiele, czyli n=0, 1, 2,.... . Oczywiście wszystkie wektory w tej przestrzeni, tj. poszczególne funkcje y _n(x) dla  n=0, 1, 2,.... , spełniają zwykłe warunki dla przestrzeni wektorowej:

1.                <a _n |a _n >≠±∞

2.                <a|b>  istnieje, gdzie <a| i <b| są dowolnymi wektorami

3.               <z| = ∑ a _n y _n(x) ,  ten warunek w istocie mówi, że dowolną funkcję reprezentowaną wektorem <z| można zbudować z funkcji bazy y _n(x).

 

Warto zwrócić uwagę, że przez iloczyn skalarny wektorów w tej przestrzeni rozumie się całkę, a nie sumę, z iloczynu funkcji definiujących składowe wektorów. Całkujemy po wszystkich składowych wektorów, tj. po argumentach funkcji.