Matematyczne obiekty „graniczne”, takie jak: punkty (tj. obiekty o zerowym wymiarze), czy zbiory nieskończenie liczne mają właściwości, które zdają się naruszać sylogizm sprzeczności.

________________________________________________________

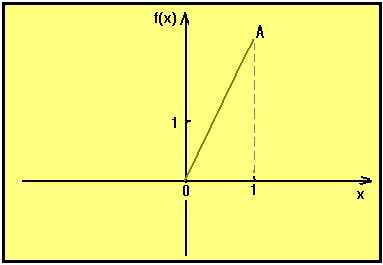
Zbiór ∞ liczby punktów można ułożyć tak, by punkty te dokładnie pokrywały odcinek (0,1) na osi x,  tj odcinek o długości 1. Ale można też tak ułożyć, by punkty te dokładnie pokrywały odcinek o dowolnej innej długości, np. ten oznaczony 0A, na rysunku. Czyli taka liczba punktów mieści się na odcinku o długości 1 i nie mieści się na takim odcinku.

 

Stanisław Banach udowodnił, że wszystkie punkty wypełniające objętość jednego jabłka można przekształcić tak, by wypełniały objętość dwu jabłek. Czyli zbiór tych punktów zajmuje objętość równą objętości jabłka i nie zajmuję objętości jednego jabłka (bo zajmuje objętość równą objętości dwóch jabłek).

 

Wiadomo, co najmniej od czasów Cantora, że zbiór liczb rzeczywistych (oznaczany symbolem C i nazywany continuum) jest liczniejszy od zbioru liczb naturalnych (oznaczanego symbolem À₀   i nazywanego alef zero). Jednak czy między À₀ ,  a  C są jakieś zbiory pośredniej liczności, czy ich nie ma? Okazuje się, że i tak, i  nie, bo można tak sformułować teorię mnogości, by odpowiedź „są”, była prawdziwa, można sformułować też tak, by odpowiedź „nie ma” była prawdziwa!